Christian Saldana

Matematicas 12mo El Olam.

Chris T Stuart

Matematicas 12mo El Olam.

Sean Paul Garcia

Matematicas 12mo El Olam.

Miguel Garcia

Matematicas 12mo El Olam.

Monday, August 27, 2012

Ejemplos De Conjuntos Usando Diagramas De Venn

4:52 PM    4 comments













  

Read More

Monday, August 20, 2012

Diagrama De Venn

5:19 PM    9 comments

Un grupo de jóvenes fue entrevistado acerca de sus preferencias por ciertos medios de transporte (bicicleta, motocicleta y automóvil). Los datos de la encuesta fueron los siguientes:
    I) Motocicleta solamente: 5
    II) Motocicleta: 38
     III) No gustan del automóvil: 9
    IV) Motocicleta y bicicleta, pero no          automóvil:3
    V) Motocicleta y automóvil pero no     bicicleta:20                                                  VI) No gustan de la bicicleta:72                          VII) Ninguna de las tres cosas: 1
    VIII) No gustan de la motocicleta: 61
  1. ¿Cuál fue el número de personas entrevistadas?
  2. ¿A cuántos le gustaba la bicicleta solamente?
  3. ¿A cuántos le gustaba el automóvil solamente?
  4. ¿A cuántos le gustaban las tres cosas?
  5. ¿A cuántos le gustaba la bicicleta y el automóvil pero no la motocicleta?
    Tratemos de volcar los datos en un diagrama de Venn para tres conjuntos.
    Nos encontraremos con que sólo cuatro de ellos (los números I), IV), V) y VII) se pueden volcar directamente:
    Ahora con el dato II) se puede completar la única zona que falta en el conjunto MOTO, haciendo la diferencia 38 - (20+5+3) = 10:



      Luego utilizaremos el dato VI), pues si consideramos todas las zonas, excepto las cuatro correspondientes al conjunto BICI, deberán sumar 72, luego 72 - (20+5+1) = 46:


      Después de ello, podremos usar el dato III), pues si consideramos todas las zonas, excepto las cuatro correspondientes al conjunto AUTO, deberán sumar 9, luego 9 - (5+3+1) =


      Por último utilizaremos el dato VIII) pues si consideramos todas las zonas, excepto las cuatro correspondientes al conjunto MOTO, deberán sumar 61, luego 61 - (46+0+1) = 14:


      Con lo que estamos en condiciones de responder a todas las preguntas:
      1. A 99 personas.
      2. A ninguna.
      3. A 46 personas.
      4. A 10 personas.
      5. a 14 personas.


Read More

Sunday, August 19, 2012

Diagrams De Venn y Subconjuntos

8:22 PM    5 comments

Historia:

 En la teoriade conjuntos comunmente utilizamos los diagramas de Venn, desarrollados por el logico John Venn. En estos diagramas el es representado por un rectangulo, y los demas conjuntos relevantes dentro de este universo se representan mediante regionaes ovaladas. Ejemplo:





U (universo) ={A , D, C, B, E, F, G, H}
A={A, B, D, E, G}
B={C, H, D, G}
C={E, D, G, F}
_____________________________
AUB={C, D}
A∩B∩C={D}
C∩A={E, D}
A’={F, G, H}
AUC={A, B, C, D, E, G}

Read More

Biografia De John Venn

7:18 PM    4 comments



John Venn


John Venn , fue un matemático y lógico británico. Destacó por sus investigaciones
 en lógica inductiva. Es especialmente conocido por su método de representación gráfica de 
proposiciones (según su cualidad y cantidad) y silogismos. Los diagramas de Venn permiten,
además, una comprobación de la verdad o falsedad de un silogismo. Posteriormente
 fueron utilizados para mostrar visualmente las operaciones más elementales 
de la teoría de conjuntos.
John Venn nació en 1834 en Hull, Yorkshire. Su madre, Martha Sykes, provenía 
de Swanland, cerca de Hull, y murió mientras John era aún muy pequeño. Su padre
 era el reverendo Henry Venn, quien en la época en que nació John era el rector de 
la parroquia de Drypool, cerca de Hull. Henry Venn venía de una familia distinguida.
 Su propio padre, el abuelo de John, el Reverendo John Venn, había sido rector de
 Clapham en el sur de Londres. Era el lider de la Secta Clapham, un grupo de cristianos
 evangélicos que se reunían en su iglesia y que promovían la reforma de la prisión y la 
abolición de la esclavitud y de los deportes crueles.
El padre de John Venn (Henry) jugó también un papel prominente en el movimiento 
evangélico. La Society for Missions in Africa and the East (Sociedad de las Misiones
 en África y Oriente) fue fundada por la clerecía evangélica de la Iglesia de Inglaterra en 
1799, y en 1812 fue rebautizada como la Church Missionary Society for Africa and the
 East (Sociedad de la Iglesia Misionaria de África y Oriente). Henry Venn fue secretario de
 la Sociedad desde 1841. Se mudó a Highgate, cerca de Londres, con el fin de llevar a
cabo sus deberes. Allí mantuvo su posición hasta su muerte en 1873.
John Venn fue criado de manera estricta. Se esperaba que siguiera la tradición familiar 
como ministro cristiano. Después de pasar un tiempo en la Escuela de Highgate, entró en 
el Colegio de Gonville y Caius, en Cambridge, en 1853. 
Se graduó en 1857 y pronto fue elegido profesor adjunto de la escuela. Fue ordenado 
diácono de Ely en 1858 y se volvió sacerdote en 1859.
 En 1862 regresó a Cambridge como profesor de ciencias morales.
El área de mayor interés para Venn era la lógica, y publicó tres textos sobre el tema. 
Escribió The Logic of Chance (Lógica del Azar), que introdujo la teoría de frecuencia de 
la probabilidad, en 1866, Symbolic Logic (Lógica Simbólica), que presentaba los 
diagramas de Venn, en 1881, y The Principles of Empirical Logic (Los Principios de 
la Lógica Empírica), en 1889.
En 1883, Venn fue elegido miembro de la Royal Society. En 1897, escribió una historia 
de su colegio, llamada The Biographical History of Gonville and Caius College, 1349–1897. 
Comenzó una compilación de notas biográfics de alumnos de la Universidad de Cambridge,
trabajo que continuó su 
hijo John Archibald Venn (1883-1958), publicado como Alumni Cantabrigienses, en
10 volúmenes, entre 1922 y 1953.

 Falleció en 1923, a la edad de 88 años, en Cambridge, y fue sepultado en el cercano 
cementerio de la Iglesia Trumpington.
Memorial de Venn en Cambridge
John Venn.jpg

Read More

Wednesday, August 15, 2012

Operaciones entre conjuntos

4:00 PM    4 comments


Operaciones entre conjuntos
La operación entre conjuntos es la unión de dos conjuntos A y B. Se define como el conjunto que contiene a todos los elementos del conjunto A y todos los elementos del conjuntó B sin repetirse.
Ejemplos: A {1,2,3}, B {3,4,5}
A͜B={1,2,3,4,5}
A͜B={x|x Ï  A o Î B}
La intersección de dos conjuntos A y B se define como el conjunto que contiene a todos los elementos que son comunes a ambos conjuntos     A y B.
Ejemplos:

ADescription: \capB={x|x Î A y x Î B}

A={1,2,3,4,5,6}

B={2,3,6,7,8,9}                 ADescription: \capB={2,3,6}

 

La diferencia de dos conjuntos A Y B  se define como el conjunto que contiene todos los elementos que están en el conjunto A, pero no están en el conjunto.

 

Ejemplos:

     A-B={x|x  Î a y x Description: \notin B}

     A-B={1,4,5}   B-A={7,8,9}

     (ADescription: \capB)-B={2,3,6}-{2,3,6,7,8,9} = Description: \emptyset 

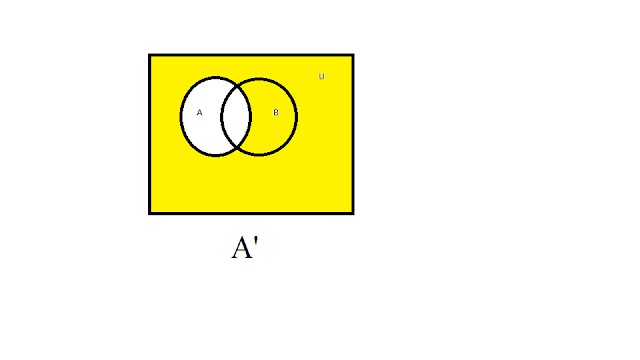
El complemento de un conjunto  A se denota y se define por : A’,=U,

-A y Ā

Producto cruzado de dos conjuntos A Y B se define como el cruce de pares ordenados de A Y B

AxB= {x|x (a,b) aÎA y b Î B}

 

Ejemplos: A={1,2,3} B={a,b}      AxB={(1,a)(1,b)(2,a)(2,b)(3,a)(3,b)

U{1,2,5,7,8,9,10,11,12,23}    A={2,5,7,8,9,11,23}   B={5,7,9,10,11,12} y c{2,7,8,11}

Read More

Tuesday, August 14, 2012

Continuacion de La Teoria de Conjuntos

3:54 PM    5 comments


El conjunto que contiene todos los elementos en una discusión determinada se le llama el conjunto universal y se denota por la letra U.                                       Ej :U= {1,2,3,4,5,6,7,8,9,10}

El conjunto A es un subconjunto propio del conjunto B, si AÍ B y A ≠ B , y se denota por ; AÌ B.         Ej:{1,3,5} Ì {1,2,3,4,5}

Dos conjuntos son iguales si tienen los mismos elementos.
                              Ej: {a,b,c} = {b,c,a}

Si W= {1,2,3,4;…,12} ; P= {2,4,6,8} y K= {3,5,4,6,2} se tiene que :

1.    P Ì W
2.    K Ì W
3.    P Í P
4.    W Í N
5.    W ≠ P
Cuando se quiere indicar que un element pertenece a un conjunto. Usamos el simbolo:
              Î se lee, es elemento de
Para indicar que el element no pertenece a un a un conjunto usamos el simbolo:
                Ï  se lee, no es element de
para indicar que un conjunto no es un subconjunto de otro conjunto usamos el simbolo
                 Ë se lee, no es subconjunto de



Read More

Monday, August 13, 2012

Elementos de la Teoria de Conjuntos

4:01 PM    4 comments

El conjunto es la reunión o colección de objetos con caracteristicas comunes. Los objetos pertenecientes se le llaman Elementos o Miembros del conjunto. Para reunir los Elementos del conjunto se usan Llaves . Adentro de la llaves los Elementos se separan con comas. 

Ej. A= {1,2,3,4,5}
B= {a,b,c,}

Las letras se ultilizan para representar los conjuntos.

Los Conjuntos se expresan de tres formas:
1. Forma Verbal
2. Forma de Lista
3. Notacion de construccion de conjuntos

El Nulo o Vacio se le dice cuando adentro de la llaves del conjunto no tiene nada
se escribe asi:
B= ø
o
B= {}
Los elementos o miembros de un conjunto pueden ser cualquier cosa números, personas, letras otros conjuntos, etc. Los conjuntos se denotan habitualmente por letras mayúsculas.

Ej. 1 Forma Verbal: El conjunto de todos los numeros enteros positivos mayores que 5 inclusive.
2. Forma enumerada: {5,6,7}
3. Notacion de construccion de conjuntos: 

{x|x ≤ 7, x es un entero positivo}
A= {1,2,3,4,5,6,7}

Los conjuntos numéricos usuales en matemáticas son: el conjunto de los números naturales N, el de los números enteros Z, el de los números racionales Q, el de los números reales R y el de losnúmeros complejos C. 
-Chris Stuart

Read More

Leonardo De Pisa (Fibonacci)- Fibonacci Y La Naturaleza

3:08 PM    5 comments



Leonardo de Pisa, Fibonacci.

 Es el que da a conocer al mundo la sucesión de Fibonacci en su libro Liber abaci, junto con el problema de los conejos.
La sucesión de Fibonacci o secuencia áurea ya había sido descubierta con anterioridad por matemáticos hindúes tales como Gopala (antes de 1135) y Hemachandra (c. 1150) quienes habían investigado los patrones rítmicos que se formaban con sílabas o nos de uno o dos pulsos. El número de tales ritmos (teniendo juntos una cantidad n de pulsos) era F(n+1), que es como sed representa al término n+1 de la sucesión de Fibonacci. Kepler también escribió sobre dicha sucesión. Y Robert Simson (en 1753) descubrió que:
F(n)/F(n-1)—>Relacion áurea cuando n tiende a infinito
La suceesión de Fibonacci es una sucesión de números de la forma:
1,1,2,3,5,8,13,21,34,55,89,…
Y su fórmula general es una función recursiva de término general
A esta fórmula se llega de forma sencilla mediante el método de diferencias divididas.Si consideramos la expresión F(n) = F(n-1)+F(n-2) y realizamos el cambio de variable x=F(n-1) llegamos a la expresión x²-x-1=0, cuyas soluciones son:
Es decir, las soluciones son el número áureo (1,618033989….) y su conjugado. Hay que tener que el número áureo es un número irracional por serlo la raíz de cinco. Este número áureo lo podemos considerar como uno de los valores propios de nuestra fórmula recursiva de Fibonacci, junto con su conjugado. Teniendo en cuenta que dichos valores propios son reales y distintos; y que nuestra forma recursiva la podemos considerar como una ecuación en diferencias, podemos averiguar la expresión de F(n) de forma explícita mediante:F(n) = a Fi^n + b fi^n , para averiguar a y b basta sustituir n = 0 y n= 2, obteniendo un sistema de dos ecuaciones con dos incógnitas, Al resolverlo nos queda que el término general de la sucesión de Fibonacci, en forma explícita es:

En la siguiente imagen podéis ver la sucesión de Fibonacci extendida al campo de los números reales.
Una de las propiedades es que cualquier número natural se puede escribir mediante la suma de un número limitado de términos de la secuencia de Fibonacci, cada uno de ellos distinto a los demás. Por ejemplo:
17 = 13+3+1, 65 = 55+8+2.
El problema de los conejos
“Una pareja de conejos tarda un mes en alcanzar la edad fértil,
a partir de ese momento cada vez engendra una pareja de conejos, que a su vez,
tras ser fértiles engendrarán cada mes una pareja de conejos.
¿Cuántos conejos habrá al cabo de un determinado número
de meses?.”
undefined
Como podéis ver en el gráfico, el número de parejas a lo largo de los meses coincide con los términos de la sucesión.La sucesión de Fibonacci En Hojas, Plantas, Flores…
Las ramas y las hojas de las
plantas se distribuyen buscando siempre recibir el máximo de luz para
cada una de ellas. Por eso ninguna hoja nace justo en la vertical de la anterior.
La distribución de las hojas alrededor del tallo de las plantas se produce
siguiendo secuencias basadas exclusivamente en estos números.
El número de espirales en numerosas flores y frutos también se
ajusta a parejas consecutivas de términos de esta sucesión: los
girasoles tienen 55 espirales en un sentido y 89 en el otro, o bien 89 y 144.
Las margaritas presentan las semillas en forma de 21 y 34 espirales.
Y cualquier variedad de piña presenta siempre un número de espirales
que coincide con dos términos de la sucesión de los conejos de
Fibonacci, 8 y 13; o 5 y 8.
Parece que el mundo vegetal tenga programado en sus códigos genéticos
del crecimiento los términos de la sucesión de Fibonacci.
La sucesión de Fibonacci Y Las Partes Corporales De Humanos Y Animales








Read More
Subscribe to: Posts (Atom)